Compound interest is interest on the interest of the initial borrowed or deposited amount. Confusing gibberish, right? For example: if a bank offers a savings account with an interest rate of 5% per year, then the final amount of interest gained at the end of a period, on the initial 100 dollars would differ, depending on how often the interest is compounded.
Interest can be compounded in various periods, usually daily, monthly, quarterly or annually. The principal amount has the interest added to it in the daily, monthly, quarterly or annual payout cycles. As soon as the interest is added, that increases the principle amount, and that full new amount then has the interest rate applied to it in full, thus continuously increasing the principle amount that has the interest rate applied to it.
There are lots of compound interest calculators to be found online. However, it is also quite simple to calculate it yourself with nothing more than the calculator on your smartphone. We think that this is a good exercise as it will help you to understand how the calculation works.
Ready for some maths?
So – lets do a calculation for having a principle amount of $1000, with an interest rate of 7% that is compounded monthly:
Firstly, convert the % interest rate into decimals. To do this use the formula: % Amount divided by 100
7/100 = 0.07
Secondly, you need to find out the the amount of interest paid per compounding period. In this case, we know that the annual interest rate is 7%. However, it is compounded monthly, so we need to calculate the amount of interest paid per month.
0.07/12 =0.0058333 per month (12 = months in a year)
Then, once you have this figure, you can then add it into the below formula – which allows you to calculate the compound interest.
1 + 0.0058333 = 1.0058333
Make a note of this number, and then, find the xy sign on your calculator:
(xy: This button is called the ‘power’ function. In this case, x refers to the initial investment and y is the period over which the interest is compounded. 12 for 12 months, 365 for 365 days.)
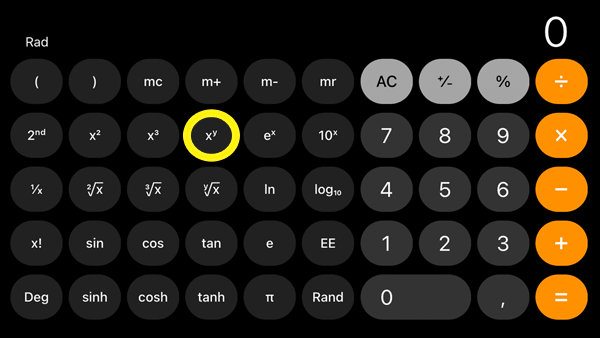
Now you are ready to do the calculation, the formula is:
Principle Amount ($1000) multiplied by 1.0058333 (the number you noted down) to the power of 12. So – on your calculator it would be:
1000 x 1.0058333.
Then press xy and enter 12.
The sum should bring = 1072.29
This means that, if you invest $1000 at the beginning of the year, and then the 7% interest is compounded monthly, then at the end of the year, you will have increased your principle to $1072.29.
The key figure here, is that if you just received 7% interest compounded annually, then you would get $1070.00. However, the extra $2.29 that you receive is the interest on your interest.
Over time compound interest really adds up
Now, that may not seem much, but if you apply that principle to longer periods, this amount can really add up. For example: Lets say you invest $1000 at the same rates as above. An annual interest rate of 7% compounded monthly. The calculation would be:
1000 x 1.0058333.
Press xy and enter 240 (amount of months in 20 years).
The result should be = 4038.71
This means that after 20 years of compounding the interest on your capital, you have increased your principal to $4038.71 – multiplying by more than 4 times! This shows the power of compound interest!
Compound interest can apply to saving accounts but also to loans, so it is imperative to always check how interest is calculated to avoid pitfalls and disappointments when it comes to loan repayments and savings.
We hope that you find this little guide helpful and enticing enough to sit down and play with the numbers yourself.